凡是过往，皆为序章

0%

MATLAB课程总结（三）

发表于 更新于 分类于 阅读次数： Valine：
本文字数： 2.1k 阅读时长 ≈ 7 分钟

这篇总结MATLAB的图形基础。

二维曲线绘图的基本操作

plot指令的基本调用格式

plot(x)

​ ◼ x为向量时，以该元素的下标为横坐标、元素值为纵坐标绘出曲线。

​ ◼ x为实数二维数组时，则按列绘制每列元素值相对其下标的曲线，曲线数

​ 等于x数组的列数。

​ ◼ x为复数二维数组时，则按列分别以数组的实部和虚部为横、纵坐标绘制多条曲线

plot(x, y)

​ ◼ x、y为同维数组时，绘制以x、y元素为横纵坐标的曲线

​ ◼ x为向量，y为二维数组、且其列数或行数等于x的元素数时，绘制多条不同颜色的曲线

​ ◼ x为二维数组，y为向量时，情况与上相同，只是y仍为纵坐标。

plot(x1, y1, x2, y2, …)

​ ◼ 绘制以x1为横坐标、y1为纵坐标的曲线1，以x2为横坐标、y2为纵坐标的曲线2，等等。

​ ◼ 其中x为横坐标，y为纵坐标，绘制y=f(x)函数曲线。

例题：

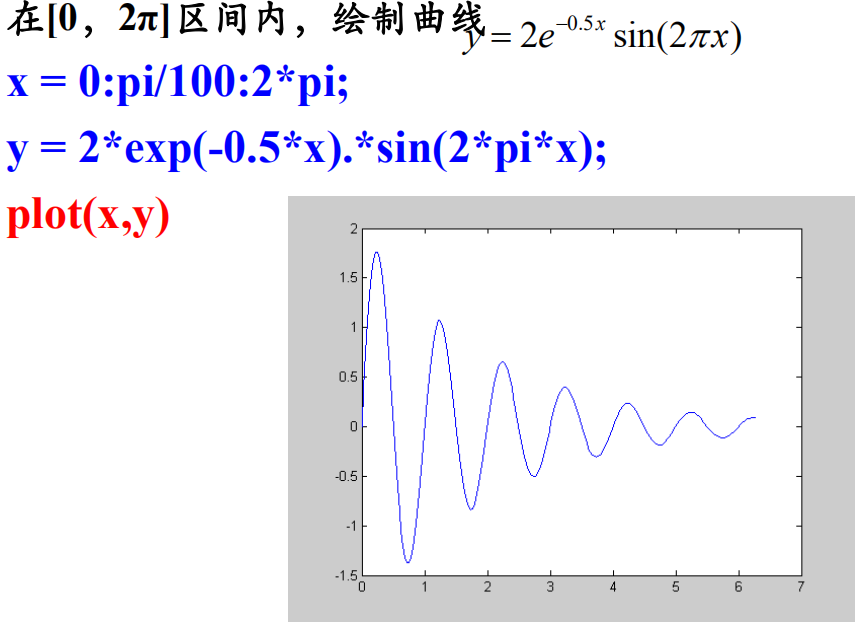
1、使用直角坐标系

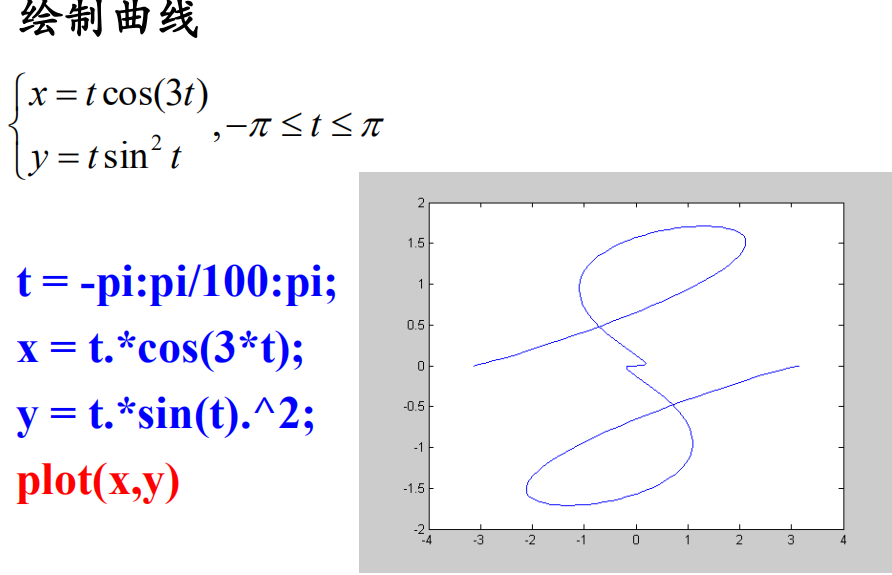
2、使用参数方程绘制曲线

3、绘制复杂曲线

结果：

多次叠绘

◼ 多次调用plot命令在一幅图上绘制多条曲线，需要hold指令的配合。

◼ hold on 保持当前坐标轴和图形，并可以接受下一次绘制。

◼ hold off 取消当前坐标轴和图形保持，这种状态下，调用plot绘制完全新的图形，不保留以前的坐标格式、曲

线。

例题1

结果

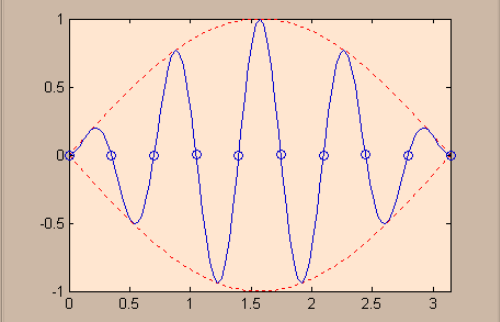
例题2：利用hold绘制离散信号的波形

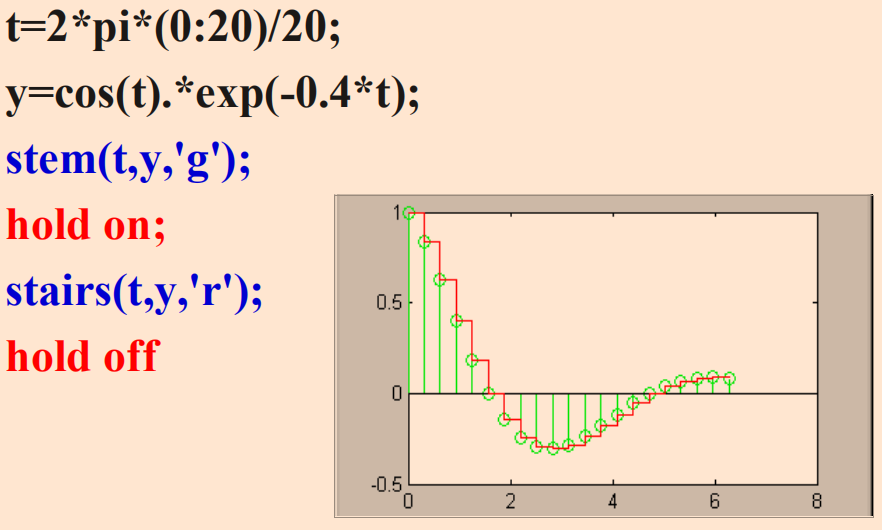
双纵坐标

◼ plotyy指令调用格式：

plotyy(x1, y1, x2, y2)

x1-y1曲线y轴在左， x2-y2曲线y轴在右。

例题

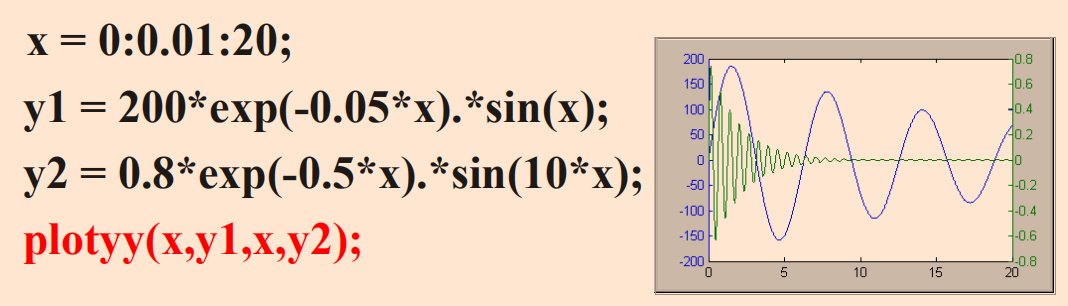
多子图

MATLAB允许在同一图形窗口布置几幅独立的子图。具体指令：

◼ subplot(m, n, k)使（mxn）幅子图中第k个子图成为当前图

◼ subplot(‘postion’, [left, bottom, width, height]) 在指定的位置上开辟子图，并成为当前图

说明：

➢ subplot(m, n, k)的含义：图形窗口包含（mxn）个子图，k为要指定的当前子图的编号。其编号原则： 左上方为第1子图，然后向右向下依次排序。该指令按缺省值分割子图区域。

➢ subplot(‘postion’, [left, bottom, width, height])用于手工指定子图位置，指定位置的四元组采用归一化的标称单位，即认为整个图形窗口绘图区域的高、宽的取值范围都是[0， 1]，而左下角为（0,0）坐标。

➢ 产生的子图彼此独立。所有的绘图指令均可以在子图中使用。

示例

1
2
3
4
5
6
t=(pi*(0:1000)/1000)';
y1=sin(t);y2=sin(10*t);y12=sin(t).*sin(10*t);
subplot(2,2,1),plot(t,y1);axis([0,pi,-1,1])
subplot(2,2,2),plot(t,y2);axis([0,pi,-1,1])
subplot('position',[0.2,0.05,0.6,0.45])
plot(t,y12,'b-',t,[y1,-y1],'r:');

结果

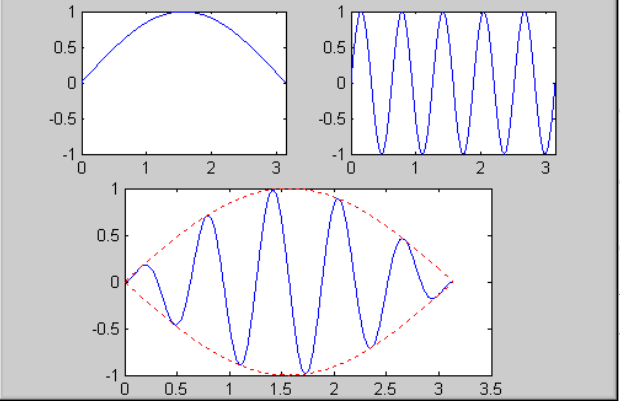
绘制曲线的辅助操作

曲线线形控制符

符号 - ： -. –
含义 实线 虚线 点划线 双划线

曲线颜色控制符

符号 b g r c m y k w
含义 蓝 绿 红 青 品红 黄 黑 白

；数据点型控制符

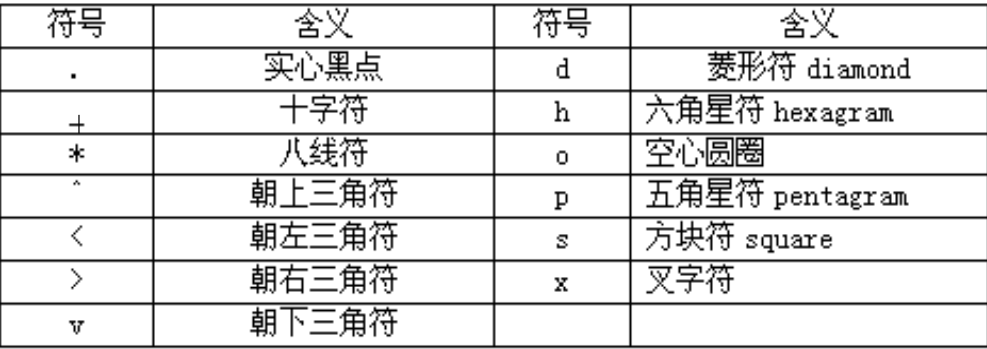
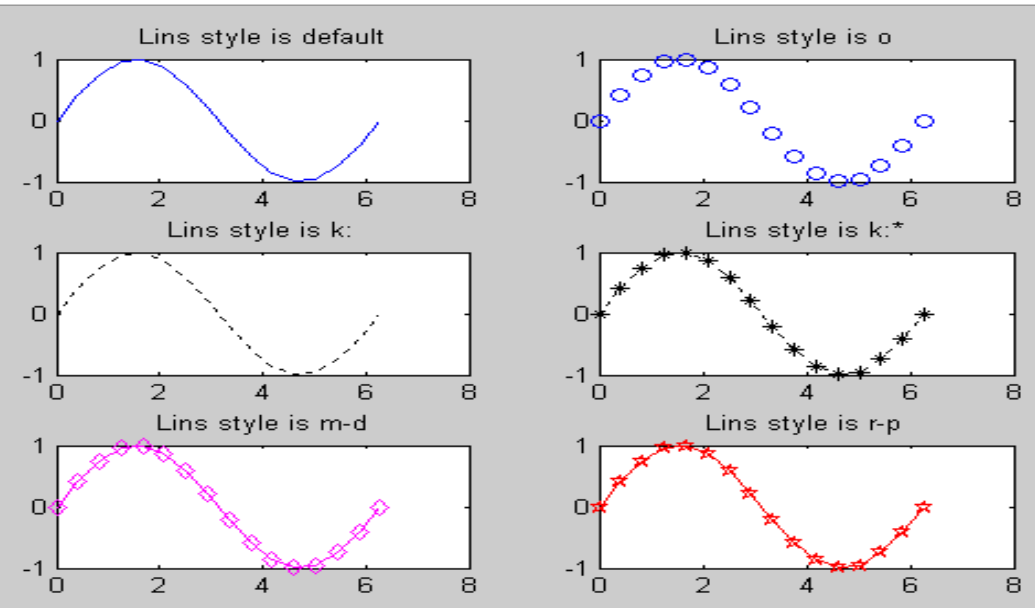
➢曲线的线形控制符、颜色控制符、数据点形控制符可以组合使用

➢其先后次序不影响绘图结果

➢也可以单独使用

例如

1
2
3
4
5
6
7
8
t=(0:15)*2*pi/15;
y=sin(t);
subplot(3,2,1), plot(t, y); title('Lins style is default')
subplot(3,2,2), plot(t, y, 'o'); title('Lins style is o')
subplot(3,2,3), plot(t, y, 'k:'); title('Lins style is k:')
subplot(3,2,4), plot(t, y, 'k:*'); title('Lins style is k:*')
subplot(3,2,5), plot(t, y, 'm-d'); title('Lins style is m-d')
subplot(3,2,6), plot(t, y, 'r-p'); title('Lins style is r-p')

坐标、刻度和分格线控制

axis坐标控制指令

案例演示

1
2
3
4
5
6
7
8
9
10
11
12
13
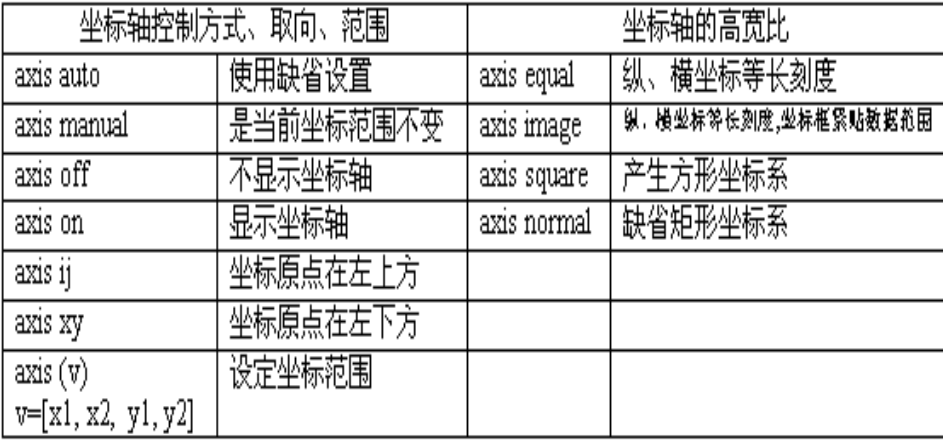
14
t=0:2*pi/99:2*pi;
x=1.15*cos(t); y=3.25*sin(t); % y为长轴，x为短轴
subplot(2,2,1); plot(x, y);
axis off
title('axis off'); 
subplot(2,2,2); plot(x,y);
axis image;
title('axis image'); 
subplot(2,2,3); plot(x,y);
axis equal;
title('axis Equal'); 
subplot(2,2,4); plot(x,y);
axis square;
title('axis Square');

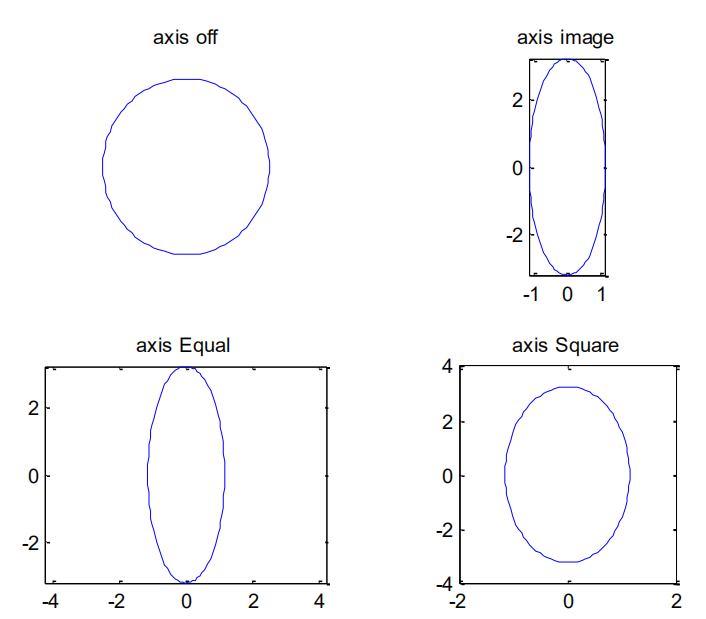
刻度、分格线和坐标框

刻度设置

  • 指令及格式：set(gca, ‘xtick’, xs, ‘ytick’, ys)

  • xs、ys可以使任何合法的实数向量，用于分别设置x、y轴的刻度。

分格线

使用grid指令

  • grid on /grid off：画出/不画出分格线
  • MATLAB的缺省设置是不画分格线；分格线的疏密取决于坐标刻度（改变坐标刻度，可改变分格线的疏密）。

坐标框

  • box on：控制加边框线
  • box off：控制不加边框线

案例

1
2
3
4
5
6
7
8
9
10
11
12
13
t=6*pi*(0:100)/100;
y=1-exp(-0.3*t).*cos(0.7*t);
tt=t(find(abs(y-1)>0.05)); 
ts=max(tt); 
plot(t,y,'r-');
grid on; 
axis([0,6*pi,0.6,max(y)]); 
title('y=1-exp(-\alpha*t)*cos(\omega*t)');
hold on;
plot(ts,0.95,'bo');
hold off; 
set(gca,'xtick',[2*pi,4*pi,6*pi],'ytick',[0.95,1,1.05,max(y)]); 
grid on;

效果

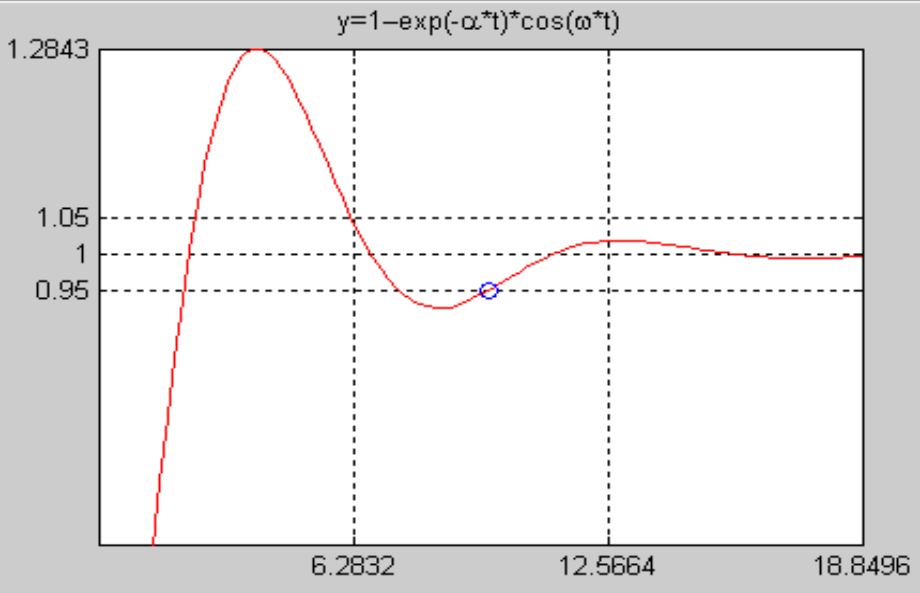
图形标识

图形标识包括

  • 图名（title）

  • 坐标轴名（xlabel、ylabel）

  • 图形文本注释（text）

  • 图例（legend）

简捷使用格式

1
2
title(s),xlabel(s),ylabel(s),text(s),legend(s) % s为字符串
text(x,y,s) 						% 指定坐标（x, y）处加注文字

精细指令形式

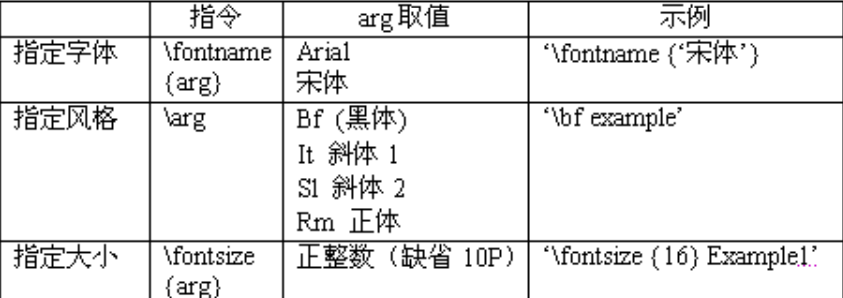
字体样式设置：

\fontname{arg} \arg \fontsize {arg} string，其中，String为要输出的字符串，其前面的均为属性控制，使用方法见下表。

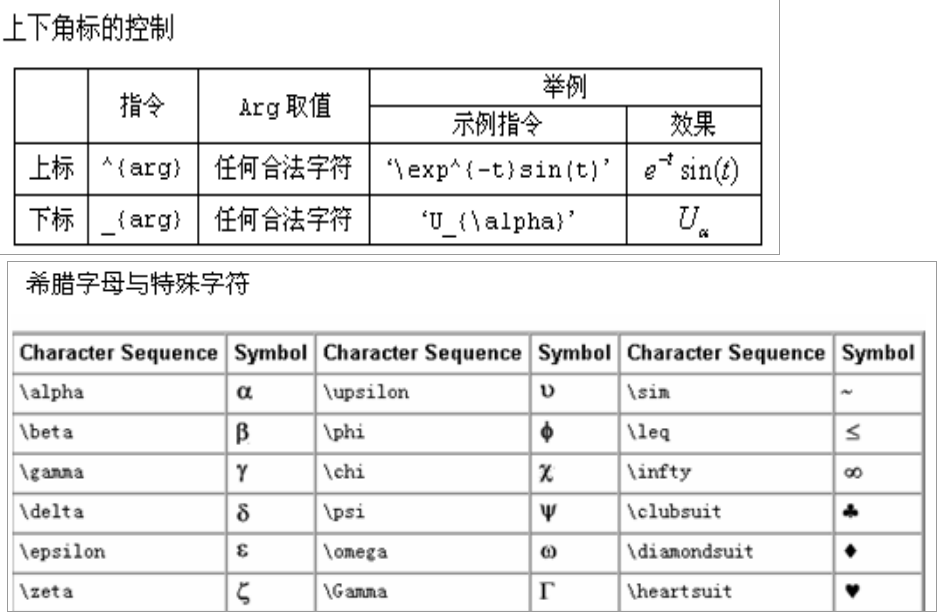
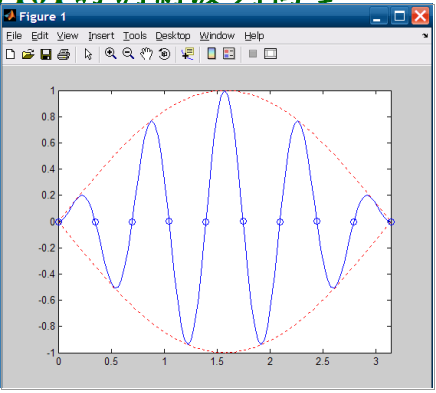
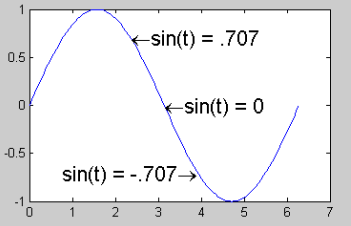
案例：在正弦曲线上标注特殊值

1
2
3
4
5
6
7
t=(0:100)/100*2*pi;
y=sin(t);
plot(t, y)
text(3*pi/4,sin(3*pi/4), '\fontsize{16}\leftarrowsin(t) = .707 ')
text(pi, sin(pi), '\fontsize{16}\leftarrowsin(t) = 0 ')
text(5*pi/4, sin(5*pi/4), '\fontsize{16}sin(t) = -.707\rightarrow',...
'HorizontalAlignment','right')

其中，‘HorizontalAlignment’, ‘right’设置图形标识为水平右对齐.

极坐标图

polar函数用来绘制极坐标图，其调用格式为：

polar(theta,rho,选项)

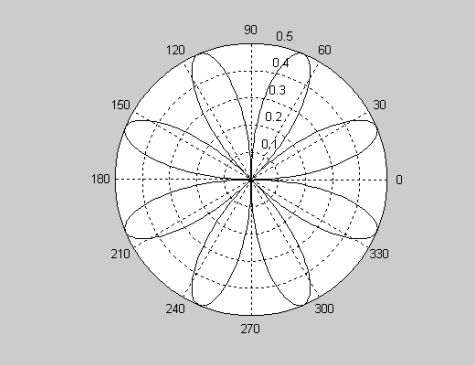
例：绘制ρ=sin(2θ)cos(2θ)的图形

1
2
3
theta = 0:0.01:2*pi;
rho = sin(2*theta).*cos(2*theta);
polar(theta,rho,'k');

结果

其他形式的线性直角坐标图

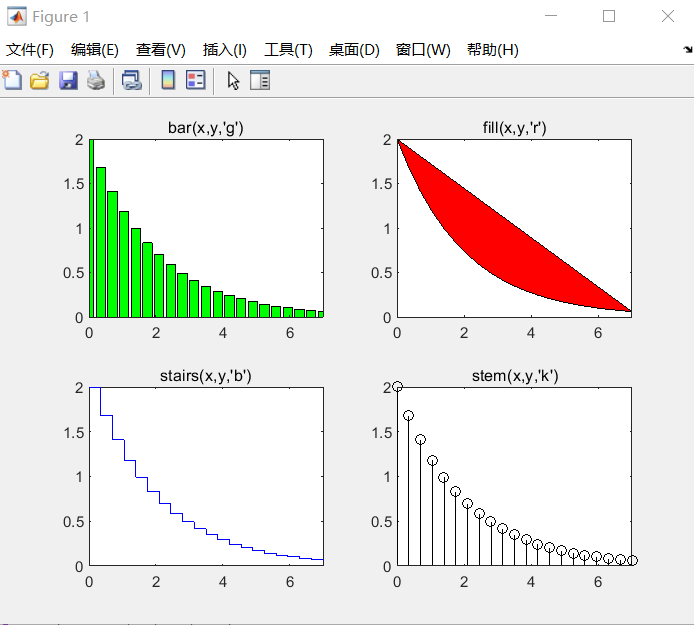
在线性直角坐标中，其他形式的图形有条形图、阶梯图、杆图和填充图等，所采用的函数分别为：

bar（x，y，选项） 选项在单引号中

stairs（x，y，选项）

stem（x，y，选项）

fill（x1，y1，选项1，x2，y2，选项2，…）

前三个函数和plot的用法相似，只是没有多输入变量形式。fill函数按向量元素下标渐增次序依次用直线段连接x，y对应元素定义的数据点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
x=0:0.35:7;

y=2*exp(-0.5*x);

subplot(2,2,1);bar(x,y,'g');

title('bar(x,y,''g'')');axis([0, 7, 0 ,2]);

subplot(2,2,2);fill(x,y,'r');

title('fill(x,y,''r'')');axis([0, 7, 0 ,2]);

subplot(2,2,3);stairs(x,y,'b');

title('stairs(x,y,''b'')');axis([0, 7, 0 ,2]);

subplot(2,2,4);stem(x,y,'k');

title('stem(x,y,''k'')');axis([0, 7, 0 ,2]);

结果

折线图、柱状图、饼图

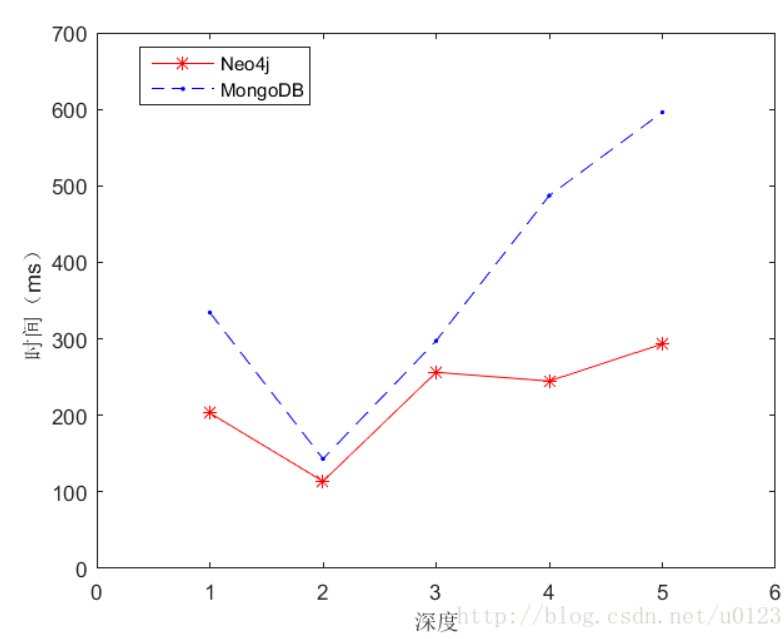
折线图

1
2
3
4
5
6
7
8
9
10
x=1:1:5;%x轴上的数据，第一个值代表数据开始，第二个值代表间隔，第三个值代表终止
 a=[203.024,113.857,256.259,244.888,293.376]; %a数据y值
 b=[334.4,143.2,297.4,487.2,596.2]; %b数据y值
 plot(x,a,'-*b',x,b,'-or'); %线性，颜色，标记
axis([0,6,0,700])  %确定x轴与y轴框图大小
set(gca,'XTick',[0:1:6]) %x轴范围1-6，间隔1
set(gca,'YTick',[0:100:700]) %y轴范围0-700，间隔100
legend('Neo4j','MongoDB');   %右上角标注
xlabel('深度')  %x轴坐标描述
ylabel('时间（ms）') %y轴坐标描述

结果

柱状图

1
2
3
4
5
6
7
8
9
10
%图12：各模式分期收益  
Y = [9.05 14.12 26.69;15.29 20.32 32.40;12.14 17.56 29.27; 10.59 15.94 28.81];% 二维数组，每一维有三个数，所以显示三种颜色，三列
figure;
bh=bar(Y);	% 画柱状图
set(gca,'XTickLabel',{'现状模式','模式一','模式二','模式三'});% 设置x轴各个柱所表示的名字
ylim([0,max(max(Y)+1)]);
legend('前期','中期','后期');	% 区分一下不同颜色分别代表什么
title('各模式分期收益（单位：亿元）');	% 标题
xlabel('模式');	% 设置x轴名称
ylabel('收益（亿元）');	% 设置y轴名称

饼图

主要是使用pie命令，pie(Y)等。

三维绘图的基本操作

三维线图指令plot3

三维绘图指令中，plot3最易于理解，它的使用格式与plot十分相似，只是对应第3 维空间的参量。

1
2
3
4
5
6
7
8
t=(0:0.02:2)*pi;
x=sin(t);
y=cos(t);
z=cos(2*t);
plot3(x,y,z,'b-',x,y,z,'bd');
view([-82,58]);
box on
legend('链','宝石')

结果

三维网线图（mesh）和曲面图（surf）

画函数z=f(x,y)所代表的三维空间曲面，需要做以下的数据准备工作：

◼ 确定自变量的取值范围和取值间隔。

➢ x=x1:dx:x2;

➢ y=y1:dy:y2;

◼ 构成x-y平面上的自变量采样“格点”矩阵。

➢ 利用MATLAB指令meshgrid产生“格点”矩阵

➢ [xa, ya]=meshgrid(x,y) ;

◼ 计算函数在自变量采样“格点”上的函数值，即z=f(x,y)。

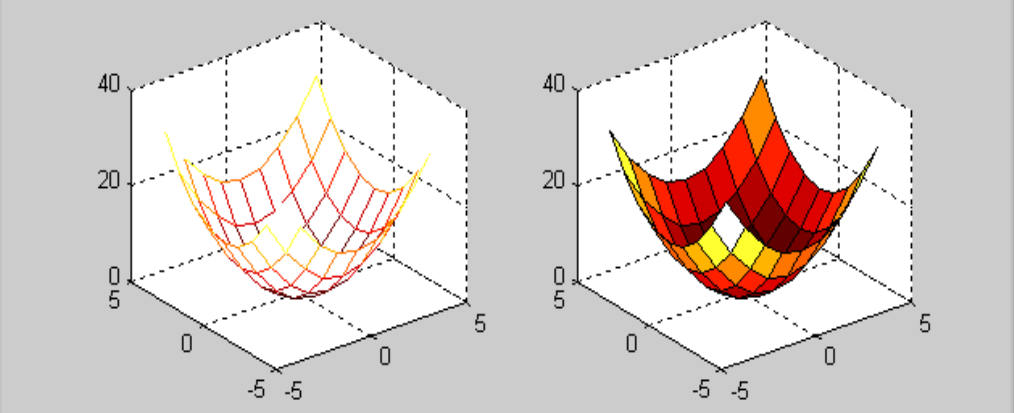
示例：绘制函数z=x^2^+y^2^的曲面

1
2
3
4
5
6
x=-4:4;y=x;
[x,y]=meshgrid(x,y); %生成 x-y 坐标“格点”矩阵
z=x.^2+y.^2; %计算格点上的函数值
subplot(1,2,1), mesh(x,y,z); %三维网格图
subplot(1,2,2), surf(x,y,z); %三维曲面图
colormap(hot);

结果

~感谢你请我吃糖果~
-------------本文结束，感谢您的阅读，欢迎评论留言！-------------