MATLAB课程总结（二）

本篇基于上篇文章基础，谈谈Matlab的数值运算，包括基本运算，与向量与矩阵处理的相关函数（最大值最小值，平均值，排序等）、多项式的相关函数（求根，加减乘除，导数等）等。

在Matlab中，一切数据均以矩阵的形式出现。相比其他语言，MATLAB在矩阵运算方面具有强大的功能，它提供了多种运算和函数对矩阵进行操作。MATLAB的数值运算包括两种：一种是针对整个矩阵的数学运算，称之为矩阵运算；另一种是针对矩阵的每一个元素进行运算的函数，称之为矩阵元素的运算。

---

一、基本运算功能

1、算术运算

• MATLAB数组支持线性代数中所有的矩阵运算。

• 建立特有的数组运算符，如：“.*”、“./”等。

2、逻辑运算

Matlab提供了3种逻辑运算符：&（与）、|（或）、~（非）。

逻辑运算符的运算法则：

1. 在逻辑运算中，确认非零元素为真（1），零元素为假（0）。

2. 当两个维数相等的矩阵进行比较时，其相应位置的元素按标量关系进行比较，并给出结果，形成一个维数与原来相同的0、1矩阵；

3. 当一个标量与一个矩阵比较时，该标量与矩阵的各元素进行比较，结果形成一个与矩阵维数相等的0、1矩阵；

4. 算术运算优先级最高，逻辑运算优先级最低。

3、关系运算

Matlab提供了6种关系运算符：<、>、<=、>=、==、~=（不等于）。

关系运算符的运算法则：

1. 当两个标量进行比较时，直接比较两数大小。若关系成立，结果为1，否则为0。

2. 当两个维数相等的矩阵进行比较时，其相应位置的元素按标量关系进行比较，并给出结果，形成一个维数与原来相同的0、1矩阵。

3. 当一个标量与一个矩阵比较时，该标量与矩阵的各元素进行比较，结果形成一个与矩阵维数相等的0、1矩阵。

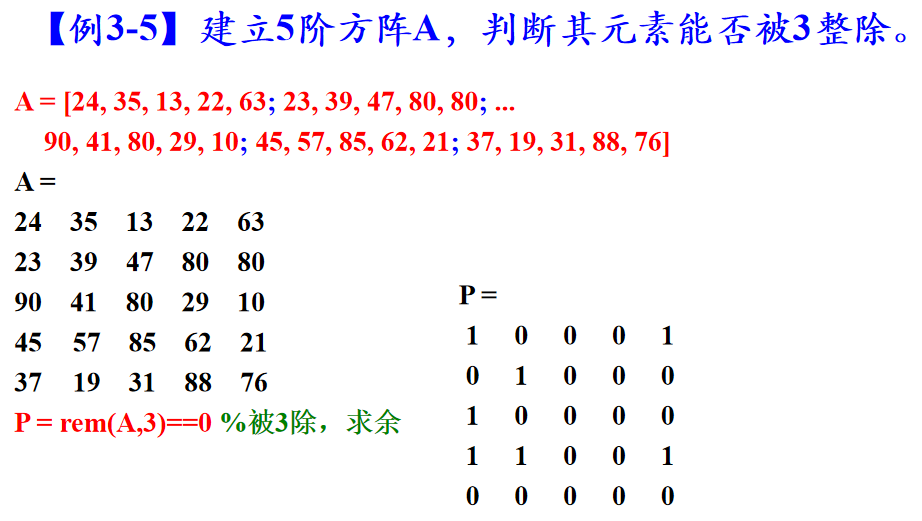
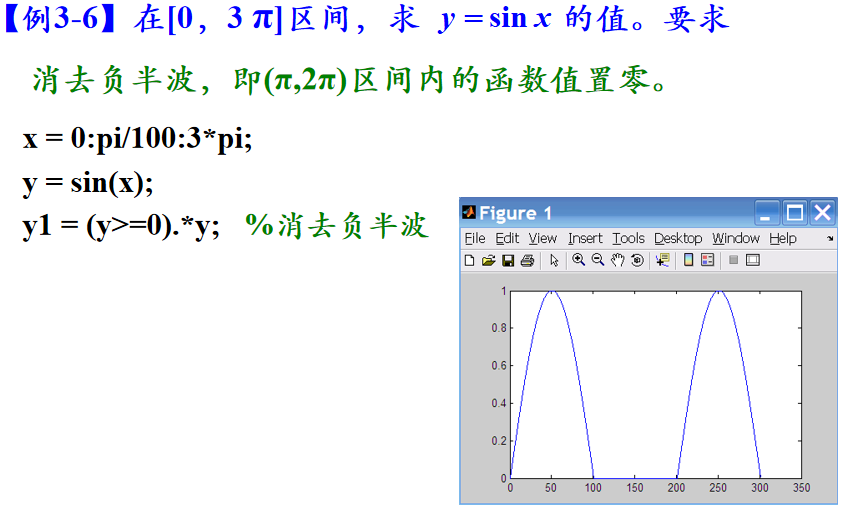
二、向量与矩阵处理相关函数

矩阵分析与处理

特殊矩阵

常见的特殊矩阵有零矩阵、幺矩阵、单位矩阵等，这类特殊矩阵在应用中具有通用性。

1、通用的特殊矩阵
常用的产生通用特殊矩阵的函数有：

• zeros：产生全0矩阵（零矩阵）。

• ones： 产生全1矩阵（幺矩阵）。

• eye： 产生单位矩阵。

• rand：产生0~1间均匀分布的随机矩阵。

• randn：产生均值为0，方差为1的标准正态分布随机矩阵。

  • 产生(0,1)区间均匀分布随机矩阵使用rand函数

  • 产生均值为0，方差为1的标准正态分布随机矩阵使用randn函数

例如：ones(5)产生5*5的单位矩阵。

1、矩阵变换函数

包括矩阵重排、矩阵抽取以及矩阵转向等。

1. 矩阵重排函数：
   reshape(A,m,n)：把矩阵A中所有元素重新排列为m*n的矩阵，矩阵总元素数必须相等。

   >> a=[1,2,3,4;5,6,7,8]
   a =
   
        1     2     3     4
        5     6     7     8
   >> reshape(a,4,2)
   ans =
        1     3
        5     7
        2     4
        6     8

2. 矩阵抽取函数：
   diag(A, k)：A为矩阵时，抽取矩阵A的第k条对角线。k可以为正整数也可以为负整数。

   >> A=[1 2 3 ; 4 5 6]
   A =
        1     2     3
        4     5     6
   >> diag(A)        % 提取A的主对角线元素
   ans =
        1
        5
   >> diag(A,1)        % 提取A的第一条对角线的元素（对角线从0计数）
   ans =
        2
     6

   同时该函数还可构造对角矩阵

   如果V是一个m个元素的向量，diag(V)将产生一个m×m对角矩阵，其主对角线元素即为向量V的元素。

   diag([1,2,-1,4])
   ans =
   	1  0  0  0
   	0  2  0  0
   	0  0 -1  0
   	0  0  0  4
   diag(1:3,-1)
   ans =
   	0 0 0 0
   	1 0 0 0
   	0 2 0 0
   	0 0 3 0

3. 矩阵转向函数：
   transpose(A)：求矩阵A的转置。可以用单引号（’）直接代替transpose函数。

   >> A=[1 2 3; 4 5 6; 7 8 9]
   A =
        1     2     3
        4     5     6
        7     8     9
   >> transpose(A)        % 求A的转置
   ans =
        1     4     7
        2     5     8
        3     6     9

2、矩阵求值函数

• inv(A)：求可逆矩阵A的逆。
• det(A)：求方阵A所对应的行列式的值。
• rank(A)：求矩阵A的秩。
• trace(A)：求矩阵A的迹。
• eig(A)：求矩阵A的特征值和特征向量。

3、数据统计与分析中的矩阵函数：

1）最大值和最小值

​ MATLAB提供的求数据序列的最大值和最小值的函数分别为max和min，两个函数的调用格式和操作过程类似。

1、求向量的最大值和最小值

求一个向量X的最大值的函数有两种调用格式，分别是：

(1) y=max(X)：返回向量X的最大值存入y，如果X中包含复数元素，则按模取最大值；

(2)[y,I]=max(X)：返回向量X的最大值存入y，最大值的序号存入I，如果X中包含复数元素，则按模取最大值。

求向量X的最小值的函数是min(X)，用法和max(X)完全相同。

>>x=[-43,72,9,16,23,47];
>>y=max(x)     %求向量x中的最大值
>>y =
>>72
>>[y,l]=max(x) %求向量x中的最大值及其该元素的位置
>>y =
>>72
>>l =
>>2

2、求矩阵的最大值和最小值

求矩阵A的最大值的函数有3种调用格式，分别是：

(1) max(A)：返回一个行向量，向量的第i个元素是矩阵A的第i列上的最大值；

(2) [Y,U]=max(A)：返回行向量Y和U，Y向量记录A的每列的最大值，U向量记录每列最大值的行号；

(3) max(A,[],dim)：dim取1或2。dim取1时，该函数和max(A)完全相同；dim取2时，该函数返回一个列向量，其

第i个元素是A矩阵的第i行上的最大值。

求最小值的函数是min，其用法和max完全相同。

>>x=[-43,72,9; 16,23,47];
>>y=max(x)     %求矩阵x中每列的最大值
y =
     16  72  47
>>[y,l]=max(x) %求矩阵x中每列的最大值及其该元素的位置
y =
    16  72  47
l =
     2  1  2
>>max(x, [],1), max(x, [],2) %求矩阵中每行的最大值

2）求和与求积

• sum(X)：返回向量X各元素的和。

• prod(X)：返回向量X各元素的乘积。

• sum(A)：返回一个行向量，其第i个元素是A的第i列的元素和。

• prod(A)：返回一个行向量，其第i个元素是A的第i列的元素乘积。

• sum(A,dim)：当dim为1时，该函数等同于sum(A)；当dim为2时，返回一个列向量，其第i个元素是A的第i行

  的各元素之和。

• prod(A,dim)：当dim为1时，该函数等同于prod(A)；当dim为2时，返回一个列向量，其第i个元素是A的第i行的各元素乘积。

3）平均值与中值

求数据序列平均值的函数是mean，求数据序列中值的函数是median。两个函数的调用格式为：

• mean(X)：返回向量X的算术平均值。
• median(X)：返回向量X的中值。
• mean(A)：返回一个行向量，其第i个元素是A的第i列的算术平均值。
• median(A)：返回一个行向量，其第i个元素是A的第i列的中值。
• mean(A,dim)：当dim为1时，该函数等同于mean(A)；当dim为2时，返回一个列向量，其第i个元素是A的第i行的算术平均值。
• median(A,dim)：当dim为1时，该函数等同于median(A)；当dim为2时，返回一个列向量，其第i个元素是A的第i行的中值。

4、元素排序

Matlab中对向量X排序的函数是sort(X), 函数返回一个对X中的元素按升序排列的新向量。

sort函数也可以对矩阵A的各列（或行）重新排序，其调用格式为：

[Y,I] = sort(A,dim)

dim=1,按列排序；dim=2,按行排序，Y是排序后的矩阵，I记录Y中的元素在A中的位置。

命令如下：

A = [1,-8,5;4,12,6;13,7,-13];
 sort(A)
 ans =
 1    -8   -13
 4     7     5
13    12     6
-sort(-A,2)  %对A的每行按降序排列
ans =
5       1    -8
12     6     4
13     7   -13

5、数据插值

在工程测量和科学实验中，所得到的数据通常是离散的，要得到这些离散点以外的其他点的数值，就需要根据已知的数据进行插值。

插值函数一般由线性函数、多项式、样条函数或这些函数的分段函数充当。

一维数据插值：被插值函数有一个单变量。

采用的方法有：线性方法、最近方法、三次样条和三次插值。

在Matlab中实现这些插值的函数是interp1，其调用格式如下：

Y1 = interp1(X,Y,X1,method)

函数根据X，Y的值，计算函数在X1处的值。

• X,Y是两个等长的已知向量，分别描述采样点和样本值；

• X1是一个向量或标量，描述欲插值的点；

• Y1是一个与X1等长的插值结果。

• method是插值方法，允许的取值为：

  （1）‘linear’：线性插值。默认的插值方式。它是把插值点靠近的两个数据点用直线连接，然后在直线上选取

  对应插值点的数据。

  （2）‘nearest’：最近点插值。根据已知插值点与已知数据点的远近程度进行插值。插值点优先选择较近的数

  据点进行插值。

  （3）‘cubic’：3次多项式插值。根据已知数据求出一个3次多项式，然后根据该多项式进行插值。

  （4）‘spline’：3次样条插值。指在每个分段内构造一个3次多项式，使其满足插值条件外，在各节点处具有光

  滑的条件。

三、多项式

1、多项式的MATLAB表达

多项式由一个行向量表示：

• 该向量元素是该多项式的系数
• 且按降幂次序排列

如：多项式x4－12x3＋25x＋116由行向量：

​ p=[1 -12 0 25 116]表示。

注意，必须包括具有零系数的项。

2、求解多项式的根？

roots指令。

>>p=[1  -12  0  25  116]
p =
     1   -12     0    25   116
>>r=roots(p)
r =
  11.7473          
   2.7028          
  -1.2251 + 1.4672i
  -1.2251 - 1.4672i

MATLAB按惯例规定，多项式是行向量，根是列向量。

3、已知多项式的根，求解多项式 ？

使用ploy指令。

>> pp=poly(r)
pp =
    1.0000  -12.0000   -0.0000   25.0000  116.0000

即：x4－12x3＋25x＋116。

4、多项式的乘法(conv指令)

举例：多项式 a(x)=x3＋2x2＋3x＋4 和 b(x)= x3＋4x2＋9x＋16 的乘积。

>> a=[1  2  3  4] ;  b=[1  4  9  16];
c=conv(a, b)
c =
     1     6    20    50    75    84    64

两个以上的多项式的乘法需要重复使用conv.

5、多项式加法

MATLAB没有提供进行加法运算的函数。

1）如果两个多项式向量大小相同，标准的数组加法有效。把多项式a(x)与上面给出的b(x)相加。

>> d=a+b
d =
     2     6    12    20

结果: d(x)= 2x3＋6x2＋12x＋20
2）当两个多项式阶次不同，低阶的多项式必须用首零填补，使其与高阶多项式有同样的阶次。
考虑上面多项式c和d相加：

>>  e=c+[0  0  0  d]
e =
     1     6    20    52    81    96    84

结果: e(x)= x6+6x5+20x4+52x3+81x2+96x+84

案例

问题：编写一个多项式加法运算的函数文件。

明确需求：

定义一个函数，需要有两个输入参数（比如：p1、p2），一个输出参数p_out。

p1、p2表示两个待计算的多项式。

p_out表示两个多项式的求和结果。

函数的内部处理：

• 若p1、p2两参数大小相等，则直接相加: p_out=p1+p2

• 若p1、p2两参数大小不等：

  • If length(p1)>length(p2)

    P2前面要补0元素，使p1、p2两参数大小相等

  • 否则

    P1前面要补0元素，使p1、p2两参数大小相等

函数文件的编写：

function p_out=poly_sum(p1, p2)
% calculate the sum of two polynomials 
 
if length(p1)==length(p2)
    p_out=p1+p2;
elseif length(p1)>length(p2)
    p2=[zeros(1,length(p1)-length(p2)), p2];
    p_out=p1+p2;
else
    p1=[zeros(1,length(p2)-length(p1)), p1];
    p_out=p1+p2;
end

6、多项式的除法(deconv)

举例说明：

c(x)=x6＋6x5＋20x4＋50x3＋75x2＋84x＋64 除以 b(x)= x3＋4x2＋9x＋16

>> c=[1     6    20    50    75    84    64];
>> b=[1  4  9  16];
>>  [q , r]=deconv(c , b)
q =
     1     2     3     4
r =
     0     0     0     0     0     0     0

7、多项式的导数 (polyder)

举例：求b(x)= x3＋4x2＋9x＋16的导数。

>> b=[1     4     9    16];
>> d=polyder(b)
d =
     3     8     9

结果为： 3x2＋8x＋9。另外两种形式为：

• p = polyder(P,Q)：求P*Q的导函数
• [p,q] = polyder(P,Q)：求P/Q的导函数，导数分子存入p,分母存入q

8、多项式的估值(polyval)

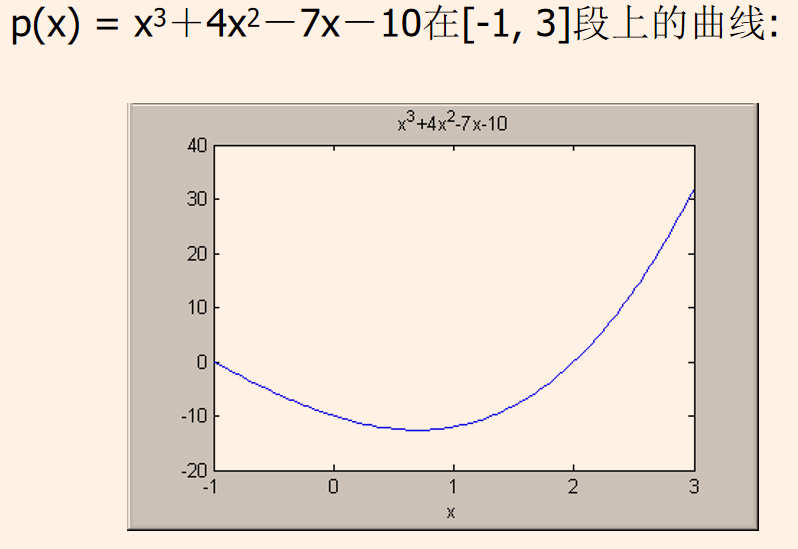
举例：绘制p(x) = x3＋4x2－7x－10在[-1, 3]段上的曲线。

x=linspace(-1, 3);  % choose 100 data points between -1and 3.
p=[1  4  -7  -10]; 
v=polyval(p, x);
 
plot(x, v);
title('x^{3}+4x^{2}-7x-10');
xlabel('x')

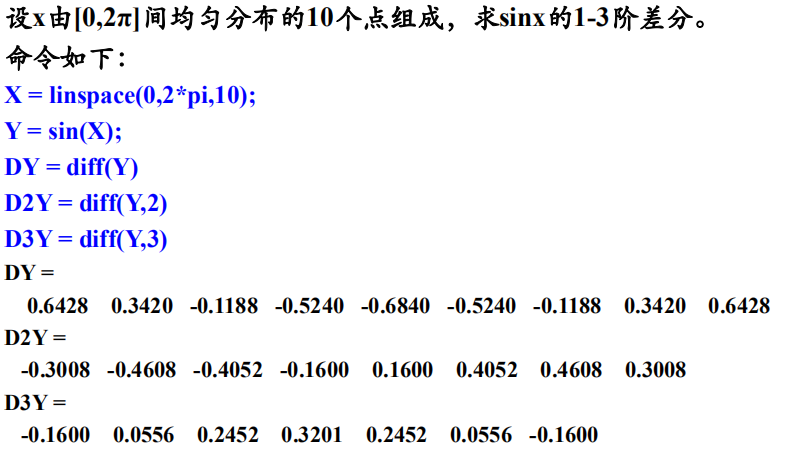
9、函数的数值导数

MATLAB中没有直接提供数值导数的函数，只有计算向前差分的函数diff，其调用格式为：

DX = diff(X) %计算向量X的向前差分
DX = diff(X，n) %计算向量X的n阶向前差分

10、数值积分

一元函数的数值积分
◼ 常用积分指令：quad和quadl。 ◼ 具体调用格式如下：

q = quadl(fun,a,b)
q = quadl(fun,a,b,tol)
q = quadl(fun,a,b,tol,trace)
[q,fcnt] = quadl(fun,a,b,...)

➢ 输入量fun为被积函数的句柄。
➢ 输入量a, b分别是积分的下限、和上限，都必须是确定的数值;
➢ 前3个输入参数是调用积分指令所必须的，其他可以缺省;
➢ 输入量tol是一个标量，控制绝对误差;
➢ 输入量trace为非0值时，将随积分的进程逐点画出被积分函数;
➢ 输出参数fcnt返回函数的执行次数。
Note：quad的调用格式与quadl相同。

案例

四、矩阵求逆与线性方程组求解

1、矩阵的逆

对于一个方阵A，如果存在一个与其同阶的方阵B，使得：A·B=B·A=I (I为单位矩阵）。

则称B为A的逆矩阵，当然，A也是B的逆矩阵。求方阵A的逆矩阵可调用函数inv(A)。

例5.18 求方阵A的逆矩阵，且验证。

A = [1,-1,1;5,-4,3;2,1,1];
B = inv(A);
A*B
ans =
   1.0000         0         0
  -0.0000    1.0000         0
  -0.0000         0    1.0000

2、用矩阵求逆方法求解线性方程组

例题：

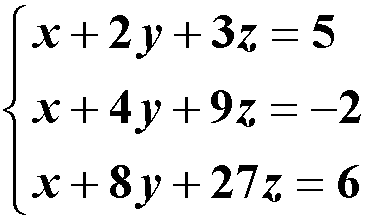
A = [1,2,3;1,4,9;1,8,27];
b = [5,-2,6]’;
x = inv(A)*b   %x = A\b
x =
  23.0000
 -14.5000
   3.6667

也可以运用左除运算符求解。